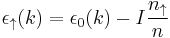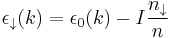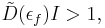Edmund Clifton Stoner

Edmund Clifton Stoner (October 2, 1899, in Surrey, England – December 27, 1968 in Leeds, England) was a British theoretical physicist. He is principally known for his work on the origin and nature of itinerant ferromagnetism (the type of ferromagnetic behavior associated with pure transition metals like cobalt, nickel, and iron), including the collective electron theory of ferromagnetism and the Stoner criterion for ferromagnetism.

Contents

Biography

Stoner born in Esher, Surrey, the son of cricketer Arthur Hallett Stoner. He won a scholarship to Bolton School (1911–1918) and then attended Cambridge University in 1918, matriculating in 1921. After graduation, he worked at the Cavendish Laboratory on the absorption of X-rays by matter and electron energy levels; his 1924 paper on this subject prefigured the Pauli exclusion principle. He was then appointed as a lecturer at the University of Leeds in 1924, and became a professor of theoretical physics there in 1939. He did some early work in astrophysics and computed a limit for the mass of white dwarf stars in 1930. Most of his research, however, was on magnetism, where, starting in 1938, he developed the collective electron theory of ferromagnetism.

He retired in 1963. The E. C. Stoner building at the University of Leeds is named after him.[1],[2],[3]

He was elected a Fellow of the Royal Society in May 1937 [4]

Stoner had been diagnosed with diabetes in 1919. He controlled it with diet until 1927, when insulin treatment became available.[1]

Stoner model of ferromagnetism

Electron bands can spontaneously split into up and down spins. This happens if the relative gain in exchange interaction (the interaction of electrons via the Pauli exclusion principle) is larger than the loss in kinetic energy.

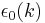\epsilon_{\uparrow} (k) = \epsilon_0 (k) - I \frac{n_{\uparrow}}{n}
\epsilon_{\downarrow} (k) = \epsilon_0 (k) - I \frac{n_{\downarrow }}{n}

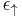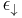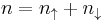where \epsilon_0 (k) is the energy of the metal before exchange effects are included, \epsilon_{\uparrow} and \epsilon_{\downarrow} are the energies of the spin up and down electron bands respectively. The Stoner parameter which is a measure of the strength of the exchange correlation is denoted I, the number of electrons is n = n_{\uparrow} %2B n_{\downarrow} . Finally k is the wavenumber as the electrons bands are in wavenumber-space. If more electrons favour one of the states this will create magnetism. The electrons obey Fermi–Dirac statistics so if when the above formula's are summed over all k-space then a criterion for ferromagnetism can be established as

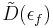\tilde{D}(\epsilon_f) I > 1,

where \tilde{D}(\epsilon_f) is the density of states at the fermi energy.

Selected publications

External links

References

  1. ^ a b Edmund Clifton Stoner, 1899-1968, L. F. Bates, Biographical Memoirs of Fellows of the Royal Society 15 (November 1969), pp. 201–237.
  2. ^ Edmund Clifton Stoner, web page at the University of Leeds, accessed December 21, 2008.
  3. ^ List of papers, collection at the Leeds University Library, accessed January 18, 2007.
  4. ^ "Library and Archive Catalogue". Royal Society. http://www2.royalsociety.org/DServe/dserve.exe?dsqIni=Dserve.ini&dsqApp=Archive&dsqCmd=Show.tcl&dsqDb=Persons&dsqPos=0&dsqSearch=%28Surname%3D%27stoner%27%29. Retrieved 22 October 2010.